什么是本福特定律?
大多数人(如果他们曾经想过的话)认为数字(例如1000或57或999或23,486,171,840,111,538)以1开头的概率与以9开头的概率相同。
本福德定律是一种观察结论,即在现实生活中许多数值数据集中,前导数字的频率不是均匀分布的。事实上,它是这样的…… 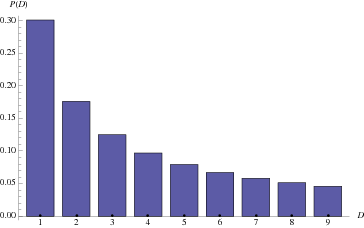
大约30%的情况下,前导数字是1。大约5%的几率是9。
如何创建本福德定律分布式数据集?
我想测试一下这个定律,所以我在1和10,000之间生成了一百万个数字,Python代码如下:
import random
#a list to store the generated random numbers
number_set = []
#Generate 100,000 random numbers
for x in range(100000):
#pick numbers between 1 and 10,000
number_set.append(random.randint(1,10001))
现在提取所有的前导数字:
##A list to store the leading digits
first_digit_set = []
#a method to get the leading digit
def get_leading_digit(number):
#convert the number to a string
#take the first character
#convert back to an integer and return the value
return int(str(number)[:1])
for d in number_set:
first_digit_set.append(get_leading_digit(d))
现在显示结果:
for i in list(range(1, 10)):
print("There are " + str(first_digit_set.count(i)) + " leading " + str(i) + "'s")
There are 33513 leading 1's
There are 33181 leading 2's
There are 33140 leading 3's
There are 33707 leading 4's
There are 33461 leading 5's
There are 33133 leading 6's
There are 33286 leading 7's
There are 33419 leading 8's
There are 33170 leading 9's

数字是均匀分布的!! 这有可能源于一下两个原因之一:
- 一位天才数学家错误地定义了他的定律
- 我做错了什么
而真正的答案则是:原来Python的标准库的随机模块生成的数字是均匀分布的。还记得本福德定律吗?它是一种观察,即现实生活中许多数字数据集的前导数的频率不是均匀分布的。 所以…
如何生成具有预定义分布的数据(使用 Python 3)?
如何使用本福德定律分布生成数据? 嗯,从Python 3.6开始random模块就有了一个名为random.choice的方法,它允许你指定权重和生成的项目数量……
from random import choices
from collections import Counter
#specify a list of values to generate occurrenced of
#these are the digits we was as leading digits
population = [1, 2, 3, 4, 5, 6, 7, 8, 9]
#Specify the weights
#these are the Benford Law weights)
weights = [0.301, 0.176, 0.124, 0.096, 0.079, 0.066, 0.057, 0.054, 0.047]
#generate sample first_digit set with Benford disctibution
#k = 10**6 generates 1 million values
first_digits = choices(population, weights, k=10**6)
#use the standard library's counter module to get the counts in order
values_in_order = Counter(first_digits).most_common()
[print(i) for i in values_in_order]
(1, 301193),
(2, 175999),
(3, 123747),
(4, 95958),
(5, 79342),
(6, 65449),
(7, 57246),
(8, 53951),
(9, 47115)

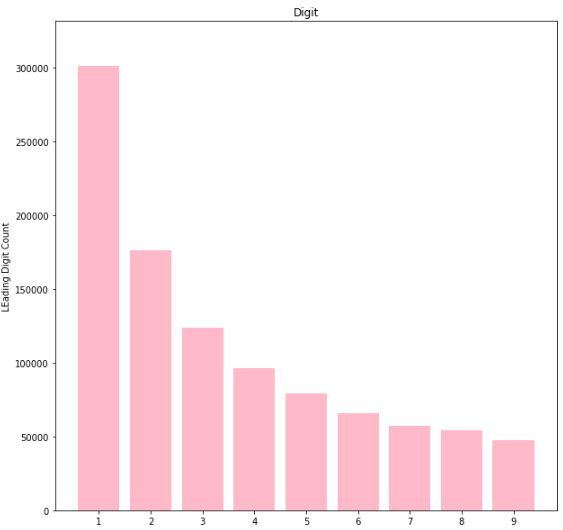
就是这样。显示本福德定律分布的100万个数字的列表。我们用图表来验证一下。
#Plot the result
import matplotlib.pyplot as plt
#For Jupyter notebooks uncomment the line below otherwise you will need to run the cell twice for the plot to appear
#%matplotlib inline
#Get the values for each digit
count = []
for c in values_in_order:
count.append(c[1])
#sets spaces to put digit count into
y_pos = population
#set size of the whole chart
plt.figure(figsize=(10, 10))
# Label the axes and the chart
plt.xticks(y_pos, population)
plt.ylabel('Leading Digit Count')
plt.xlabel('Digit')
plt.title('Benford\'s Law Distribution')
# Create bars and choose color
plt.bar(y_pos, count, color = 'pink')
# Limits for the Y axis
plt.ylim(0, int(max(count)*1.1))
#Display the Bar Graph
plt.show()